All About Shear Modulus

Shear modulus is the ratio of shear stress (force per unit area) to shear strain (displacement at the edge). It is an indication of a material’s rigidity and its resistance to deformation due to shear stress. Values for shear modulus range from as high as 520 GPa for diamond to the neighborhood of 10 - 80 GPa for common metals, all the way down to below 1 GPa for polymers and rubbers. This article will describe the shear modulus, give some examples, and explain how it is calculated.

What Is Shear Modulus?

Shear modulus is defined as the ratio between shear stress and shear strain. It is calculated as the shear force per unit area divided by the displacement of the edge of that material. Shear modulus is often referred to as the modulus of rigidity, as it gives an indication of how rigid the material is (in other words, how much it resists deformation from a shear force).

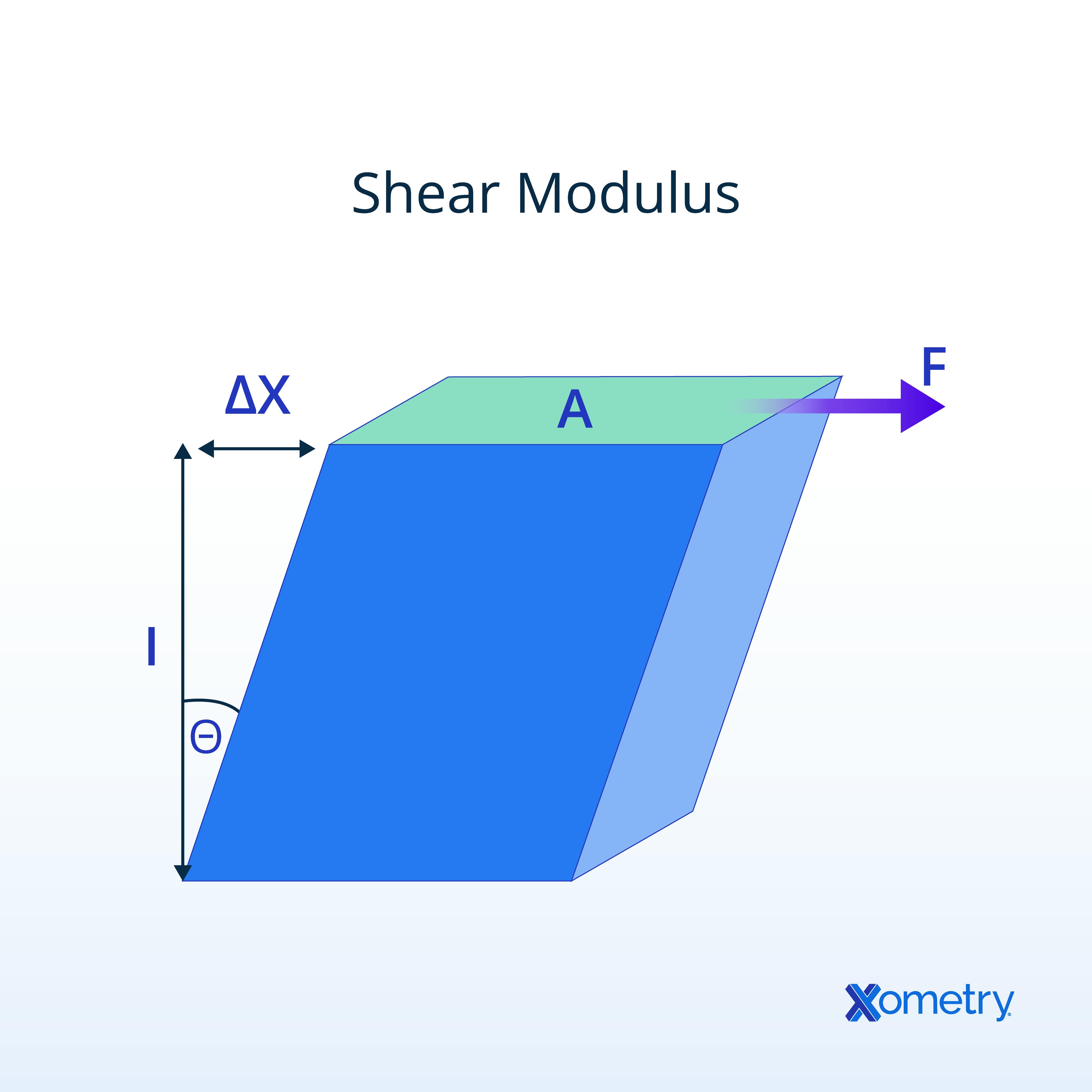
This is different from Young’s modulus (or the modulus of elasticity), which refers to a material’s resistance to deformation from a tensile or compressive force. However, these concepts (together with that of bulk modulus under uniform force or pressure) all stem from Hooke’s law. Robert Hooke determined in the 17th century that the deformation experienced by a material (in his case, a spring) was proportional to the force applied to it.

The concept of shear modulus developed further when, in the 19th century, Augustin-Louis Cauchy derived the shear modulus equations. The experimental methods to measure the shear modulus were only developed in the early 20th century.

The SI (Système International) unit for shear modulus is Pascal (Pa), the same as that for pressure. Due to the commonly measured values, however, most shear moduli are reported in units of gigapascal (GPa), which is 1x109Pa.

An example of shear modulus occurs in the structural steel used to create large buildings. Structural steel needs to withstand tensile and compressive forces, both of which are easy to account for via Young’s modulus. However, outside forces such as wind loading can put twisting stresses on the structure. This induces shear stresses in the steel members. Steel is chosen as the material for these structural members because of its very high shear modulus. It is incredibly rigid and resistant to deformation caused by shear forces.

Shear Modulus Values

A range of shear modulus values for various common materials is given in Table 1 below:

Metals have relatively high shear moduli, ranging from lead (for example) on the softer side, to stainless steel on the more rigid end. Other materials like concrete, glass, and wood exhibit similar rigidity values but fall toward the lower end of the scale. With plastics, the shear modulus is an order of magnitude lower, showing notably low rigidity values. Rubber is given as an example of a solid (viscoelastic) material that is valued specifically for its low rigidity.

The values of shear modulus are expressed most often in Gigapascals. The modulus is the ratio between the shear stress exerted on the material (as a force per unit area) and the shear strain (or displacement) of the material surface. The result is expressed as a single value, technically in units of Pascals. However, because most useful shear modulus values (of common metals, for example) are in the range of 5x1010 Pa, values of shear modulus are usually expressed using units of Gigapascals (GPa). That turns a cumbersome 5x1010 Pa value into a shear modulus of 50 GPa, making it much easier to report.

Values of shear modulus can also be expressed in units of psi, but the values then need to be given in scientific notation due to their size. Our example shear modulus of 50 GPa would thus be expressed as 7.3x106 psi.

• High Shear Modulus: A high shear modulus indicates a very rigid material — one which is not easily deformed by significant stress. This indicates that the material is hard. A shear modulus above 50 GPa is broadly considered high, as most soft metals have shear moduli of 40 GPa or lower. However, the moniker of high or low modulus depends heavily on its specific application. Its shear modulus needs to be considered against the needs of the application and the other materials that will share its engineering space. 
• Low Shear Modulus: A low shear modulus indicates a material that is relatively easy to deform. A small amount of stress (force per unit area) exerted on the material will distort it. Generally speaking, any shear modulus below 10 GPa could be considered low — a single human will be able to deform such material by hand without much trouble. However, the suitability of any material’s shear modulus must be judged relative to its application and to the potential alternative materials one might consider.

Diamond has the highest known shear modulus, usually reported in the range of 480-520 GPa. This is an order of magnitude higher than most metals. Diamond also has the highest Young’s modulus, making it renowned as the hardest natural material in the world. Diamond is very stiff; even when placed under large stresses (forces) it will experience very little displacement (the strain is low).

Diamond has the highest shear modulus due to the covalent bonds in its carbon lattice. The carbon atoms form a specific diamond cubic crystal structure which packs them in very tightly and thus makes the lattice very hard. However, diamond is not particularly resistant to breaking because they can be cleaved along specific planes.

Shear Modulus Calculation

Different tests can be used to determine shear modulus, with a number of variations in equipment and method depending on the nature of the material being tested. Most tests for solid materials are based on rotational torsion of rods or hollow cylinders. The ASTM D2236 standard, for example, uses a hollow cylinder with a pendulum (large disk) on the end and imparts a torsion (rotation) on the disk first in one direction, then the other. You can calculate the shear modulus by measuring the period of this torsion pendulum (i.e. the time between peaks).

Another method is a static torsion test. This test uses a rod of the material, twists it by a set angular distance, and then measures the stress. In this way, a stress vs strain relationship can be plotted for the material. Various ASTM standard testing methods apply a static torsion test to measure shear moduli, such as ASTM E143 for structural materials, or ASTM A938 for metallic wire as examples. 

Shear modulus is represented by an uppercase letter G. In some contexts, the symbols S or μ have also been used for shear modulus, but they are less common. The equation for shear modulus is as follows: 

It is the ratio of shear stress (τ) to shear strain (γ) in the xy plane.

Shear Modulus vs. Young’s Modulus

To understand the difference between shear modulus and Young’s modulus, we must first understand that Young’s modulus is the ratio of stress (specifically compressive or tensile stress) to strain. It indicates the stiffness of a solid and is also referred to as the modulus of elasticity.

Shear modulus is a similar concept, but describes the ratio of stress to strain under shear forces rather than compressive or tensile forces. It is therefore not the same measurement as Young’s modulus but often has a similar value. Shear modulus is sometimes referred to as the modulus of rigidity.

The two moduli are typically related to each other, as is the bulk modulus found using Poisson’s ratio. Assuming that the material obeys Hooke’s law for each of these properties (that the strain is proportional to the stress applied), each value can be approximated via the following relationship:

2G(1+υ) = E = 3K(1−2υ)

Where:

G - shear modulus

E - Young’s modulus

K - bulk modulus

υ - Poisson’s ratio

Disclaimer

The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.