Flexural Modulus: Definition, Calculation, and Importance

The flexural modulus of a material is a critically important parameter because it enables engineers to quantify the amount of bending load a component can sustain without undergoing excessive deformation. This property plays a key role in designing safe and reliable structural elements and mechanical parts.

An error in the calculation or application of flexural modulus can lead to structural failure or compromised performance, potentially resulting in costly or dangerous consequences. Therefore, it is essential for engineers, designers, and builders to thoroughly understand what flexural modulus is, how it is determined, and how it influences material behavior under bending loads.

This article will define flexural modulus, explain how it is calculated, and describe its significance in engineering design and material selection.

What Is Flexural Modulus?

The flexural modulus (sometimes referred to as the bending modulus or tangent modulus) of a material is a mechanical property. It describes its stiffness or resistance to a bending action or its ability to deform in bending. Specifically, the flexural modulus is the ratio of stress (the force applied over a specific area) to strain (the change in length over the original length) experienced by a material during bending, where tension and compression occur on opposite sides of the material. The flexural modulus of a material is dependent on its chemical composition and the arrangement of atoms throughout its structure. A higher flexural modulus indicates a material is more resistant to bending. In comparison, a lower flexural modulus indicates a material has a higher tendency to bend when a given amount of bending stress is applied.

How To Determine the Flexural Modulus of a Material

The flexural modulus of a material is commonly determined using the ASTM D790 standard, published by the American Society for Testing and Materials (ASTM). This procedure outlines the testing method for evaluating the flexural properties of both reinforced and unreinforced plastics, including thermoplastics, thermosets, composites, and electrical insulation materials.

ASTM D790 describes a three-point bending test in which a rectangular specimen is supported at both ends, and a load is applied at the midpoint. As the force increases, stress (plotted on the y-axis) is recorded against strain (x-axis), producing a stress-strain curve. The relationship between stress and strain is initially linear, representing the material's elastic behavior. This linear region is used to determine the flexural modulus. According to ASTM D790, the modulus is calculated from the slope of this linear portion, typically using a best-fit line rather than a single-point ratio of stress to strain. 

Accurate determination requires controlled test conditions, including specified loading rates, support spans, and specimen dimensions. These parameters are crucial for ensuring consistency and comparability of results across different materials and test setups.

What Is the Formula for Flexural Modulus?

The flexural modulus (also called the modulus of elasticity in bending) quantifies a material's stiffness during bending. It is defined using the following formula derived from beam theory:

Where:

1. E  is the flexural modulus (in Pascals, Pa)
2. L is the support span (length between the two supports)
3. F is the applied force at the center of the specimen
4. 𝑤 is the width of the specimen
5. ℎ is the height (or thickness) of the specimen
6. 𝑑 is the deflection at the midpoint due to the applied force

For isotropic materials, Eflex is equal to Young’s Modulus of the material due to the derivation of the elastic beam theory and the second moment of inertia for a rectangular beam.

What Are the Units of Flexural Modulus?

Flexural modulus has the same units as stress, typically MPa or psi. The flexural modulus is the ratio of stress to strain. Since strain is a unitless value, the flexural modulus ends up with units of MPa or psi.

What Is the Symbol for Flexural Modulus?

The letter “E” denotes the flexural modulus of a material. However, the letter “E” also refers to another value: the modulus of elasticity (Young’s modulus). If both the flexural modulus and the modulus of elasticity are described in the same document, the flexural modulus is differentiated by using the term Eflex.

What Is the Importance of Measuring Flexural Modulus?

Measuring flexural modulus is important because it allows engineers to quantify a material’s stiffness when subjected to bending forces. This property is critical in applications where rigidity or flexibility directly influences structural performance. Certain designs require materials to be strong and rigid to maintain structural integrity under load, while others benefit from materials that are flexible and capable of absorbing deformation without failure.

Understanding a material's flexural modulus enables engineers to predict its behavior under bending stresses, allowing for the design of safe, efficient, and application-specific components and structures. It is particularly vital in industries such as automotive, aerospace, civil engineering, and consumer products, where mechanical performance under load is a key design factor.

What Is the Flexural Modulus of Plastics?

The flexural moduli of plastics vary greatly. Some plastics, such as LDPE (Low-density Polyethylene), are more flexible, while others, like fiber-reinforced Nylon 12, are more rigid. The flexural modulus for LDPE is 335 MPa, while the flexural modulus for fiber-reinforced Nylon 12 is 13,700 MPa. The flexural modulus for most plastics falls between these two values.

What Is the Flexural Modulus of Steel?

Regarding plastics, the flexural modulus of steel varies depending on the specific type of steel in question. For steels, the flexural modulus can vary from 16,400 MPa to 106,000 MPa, depending on the steel’s composition and heat treatment condition, as well as its thickness.

Is There a Device Used To Measure Flexural Modulus?

Yes, there is a device used to measure the flexural modulus. Material testing systems, such as tensile test machines or compressive test machines, can be used to measure flexural modulus.

How Does Flexural Modulus Relate to 3D Printing?

The flexural modulus of different 3D printing materials and their print orientation has a significant impact on the ability of a 3D-printed part to bend. Ensure the print layers are made perpendicular or normal to the direction of the intended force when 3D-printing a part that may be subjected to varying loads. This is to improve the rigidity of the part and its resistance to bending.

Considering a 3D-printed horizontal bar with a force centrally applied at a point along its length, the points that experience the highest amounts of stress are the top and bottom surfaces of the part. Because the part’s layers are printed normally to the direction of the applied force, it will be more resistant to bending and thus, have a higher flexural strength. Conversely, if the part’s layers were made parallel with the applied force, it would be easier for the layers to delaminate and rupture, consequently destroying the part.

Do I Need To Test the Flexural Modulus of 3D Printing Materials?

No, it’s not necessary to test the flexural modulus of 3D printing materials. Many filament and photopolymer manufacturers publish flexural modulus data on their 3D printing materials.

What Are the Two Types of Flexural Modulus Tests?

There are two types of tests for determining the flexural modulus of a material. They are described below:

1. 3-Point Bending Test

A 3-point bend test set-up consists of two fixed supports, one at each end of a test specimen, and a rounded contact point to transmit force through a load cell to the mid-span of the test bar. The specimen bends in the shape of a “V” as the applied force increases. The 3-point bend test is often used for homogeneous materials that yield or break at strain rates of less than 5%. This includes materials like non-fiber-reinforced plastics.

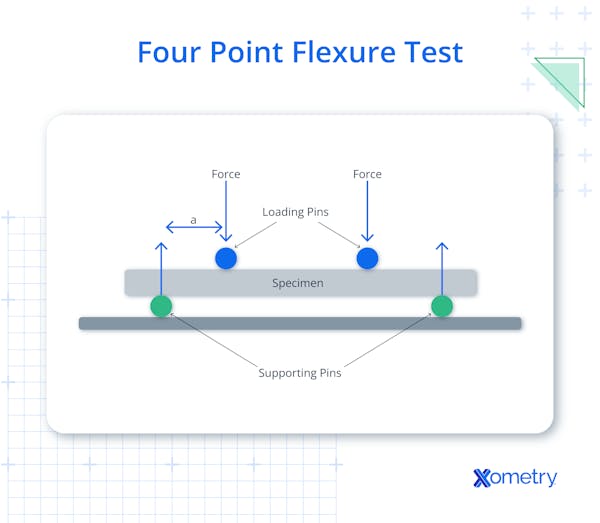
2. 4-Point Bending Test

The 4-point bend test is also performed on a test specimen that is supported at two opposite ends. But rather than a force being applied at a single point at mid-span, the force is applied at two points. This causes the specimen to bend in the shape of a “U”. The 4-point bend test is suitable for non-homogeneous materials that must exceed 5% strain to break or yield. This includes materials such as composites and wood.

What Does a Lower Flexural Modulus Mean?

A material with a lower flexural modulus is flexible or less resistant to bending than one with a higher flexural modulus. A lower value for this characteristic means that a material deforms more in response to a given applied stress.

What Does a Higher Flexural Modulus Mean?

A higher flexural modulus indicates that a material is rigid or more resistant to bending than one with a lower flexural modulus. A higher flexural modulus means a material deforms less in response to a given applied stress.

What Materials Are Commonly Tested for Flexural Strength?

Flexural strength is not the same as flexural modulus, but is obtained using the same methods. Flexural strength is the strength, or stress, at which a material breaks during bending. The materials commonly tested for flexural strength are listed below:

1. Concrete

Concrete is a material that is commonly tested for flexural strength due to the loading conditions it experiences in its typical applications and its extensive use in various construction projects. It is widely used for beams, bridges, and sidewalks where bending is common due to the loads applied. The flexural strength of concrete is often estimated to be 10-20% of its compressive strength. Flexural strength for concrete is determined using the 4-point test method.

2. Ceramics

Ceramics, like concrete, are materials that tend to break at lower stresses compared to materials like plastics and metals. The flexural strength of ceramics is often tested because of the types of stresses they experience in their typical applications. Ceramics are frequently used for structural applications such as bricks, roof tiles, and floor tiles. Flexural strength for ceramics can be obtained using the 4-point bending test. Flexural strength values range from 5 to 70 MPa.

3. Composites

Composites are materials that have several constituents. This includes materials such as plywood, reinforced concrete, and reinforced plastics. Composites are often tested for flexural strength due to their extensive use in various structural and load-bearing applications, such as building columns, beams, and frames. The flexural strength of composites can be determined using 4-point bending tests. Values for the flexural strength of composites vary depending on the material being examined. For example, a composite material composed of fiber-reinforced 65% nylon 6,6, 30% polypropylene, and 5% glass fiber has a flexural strength of 32 MPa.

4. Plastic Materials

The flexural strength of plastics is commonly tested because of the types of loads plastics experience in applications where a certain degree of flexibility or stiffness is required. Flexible plastics are used in many applications, including weather seals, diving equipment, medical catheters, and cell phone cases. Rigid plastics are used in various applications, including automotive parts, gears, furniture, plumbing systems, and other items. Flexural strength for plastics can range from 40 to 1000 MPa, depending on the type of plastic.

Summary

This article presented flexural modulus, explained what it is, and defined the formula needed to calculate it. To learn more about flexural modulus, contact a Xometry representative.

Xometry provides a wide range of manufacturing capabilities, including 3D printing and other value-added services for all of your prototyping and production needs. Visit our website to learn more or to request a free, no-obligation quote.

Disclaimer

The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.