Stress and strain are two of the most important concepts in materials science and engineering. Stress refers to the force applied to a material per unit area, while strain is a deformation or change in the shape of the material that results from the applied force. However, the relationship between stress and strain is not always straightforward. Different materials can exhibit very different stress-strain behaviors depending on their composition, structure, and loading conditions.
This article will explore the key differences between stress and strain and why they matter for engineering and design. We'll discuss the different types of stress and strain, how they're measured and analyzed, and how they can be used to predict the performance and failure of materials and structures.
What Is Stress?
Stress is defined as the force per unit area that acts on a material. This property helps define how different materials behave under specific loading conditions.
Various types of stress can occur inside an object, including compressive stress, tensile stress, shear stress, and torsional stress, among others. Different symbols are used to represent each type of stress, with the Greek letter sigma (𝜎) being the primary symbol. The mathematical expression for stress is given below:

Where:
- σ is stress, measured in N/m² or Pa
- F is the applied force, measured in Newtons (N)
- A is the cross-sectional area to which the force is applied, measured in m²
Additional symbols include 𝜎t, 𝜎c, and 𝜏, which represent tensile stress, compressive stress, and shear stress, respectively.
Additional symbols include 𝜎t, 𝜎c, and 𝜏, which represent tensile stress, compressive stress, and shear stress, respectively.
How Stress in Materials Works
Stress within an object, structure, or material develops when an object is subjected to a deforming force. As a result of the applied force, it undergoes either elastic (reversible) or a combination of elastic and plastic (permanent) deformation. The bonds between atoms of a material resist external forces, developing an equal and opposite reaction force inside the stressed object.
Even the application of a simple tensile force, stretching a material along just one of its axes, results in reaction stresses generated in at least two dimensions, since the material is elongating in one direction and contracting in a direction normal to the applied force. The real three-dimensional stress state of an object under load is represented by a stress tensor, which describes the stress state in each of the principal directions as well as the interactions between the stresses on the principal axes.
How Stress of Materials is Measured
Measuring stress directly is not possible, so instead, we must measure either the applied forces or resulting deformations. To measure deformation, it is necessary to have an understanding of the relationship between the applied forces (stresses) and the resulting deformations (strains).
Several experimental testing techniques and instruments can be used to indirectly measure the generation of stress by applied forces, such as strain gauges, extensometers, piezoelectric materials, load cells, ultrasonic testing, x-ray diffraction, and photoelasticity.
Once the magnitude of the force is known, or measured, the stress equation (σ=F/A) can be used to calculate stress.
Stress analysis is a valuable tool for evaluating the effects that various forces can have on an object, and it can be performed using various techniques, such as experimental testing, computational simulations, analytical mathematical modeling, or a combination of these methods. The choice of technique depends on the material being tested, the type of stress measured, and the desired level of accuracy.
What Is Strain?
Strain is a measure of the deformation of a material under the influence of an external force. It represents the amount of deformation that occurs in a material when subjected to stress. Strain is defined as the ratio of the change in length (or other dimensions) of a material to its original length (or dimension), and is expressed as a unitless quantity or as a percentage. The equation in terms of change in a specimen’s length is given below:

- Strain (ε) is the fractional or percentage change in length or another dimension.
- L is the length of the material after an external load is applied.
- L0 is its original length measured in the same units as “L”.
The name for the type of strain observed is based on the name for the type of stress applied: tensile strain, shear strain, compressive strain, volumetric strain, and thermal strain. A tensile strain occurs when a material is stretched or elongated, while compressive strain occurs when a material is compressed or shortened. A shear strain is the result of stress applied in a direction parallel to the cross-section of interest. Volumetric strain relates to changes in the volume of a material due to changes in its shape or size. Lastly, thermal strain refers to the change in length or volume of a material due to temperature changes.
How Strain in Materials Works
When an external force is applied to a material, it causes deformation, which is measured as strain. The deformation behavior of the material under stress depends on various factors such as the type of material, its composition, and the magnitude, direction, and nature of the applied stresses. In general, materials can deform in three main ways under stress:
- Elastic Deformation: Occurs when the material deforms under stress but returns to its original shape when the stress is removed. In other words, the material can withstand a certain amount of strain without undergoing permanent deformation.
- Plastic Deformation: Occurs when the material is subjected to stress beyond its elastic limit, causing permanent deformation. The material undergoes a change in shape that is not recoverable even after the stress is removed. The amount of plastic deformation that a material can undergo before it breaks is known as its ductility.
- Fracture: Occurs when the applied stress exceeds the strength of the material, causing it to break or fail. The strength of a material indicates its ability to withstand stress without breaking or undergoing plastic deformation.
How Strain of Materials is Measured
Various methods can be used to measure strain. The most popular methods are strain gauges and extensometers. Both of these methods require contact between the specimen and the instrument, and both are directional. Other methods that can be used include digital image correlation (DIC), piezoelectric sensors, and acoustic emission sensors.
Key Differences of Stress and Strain
The key differences between stress and strain and listed in the chart below:
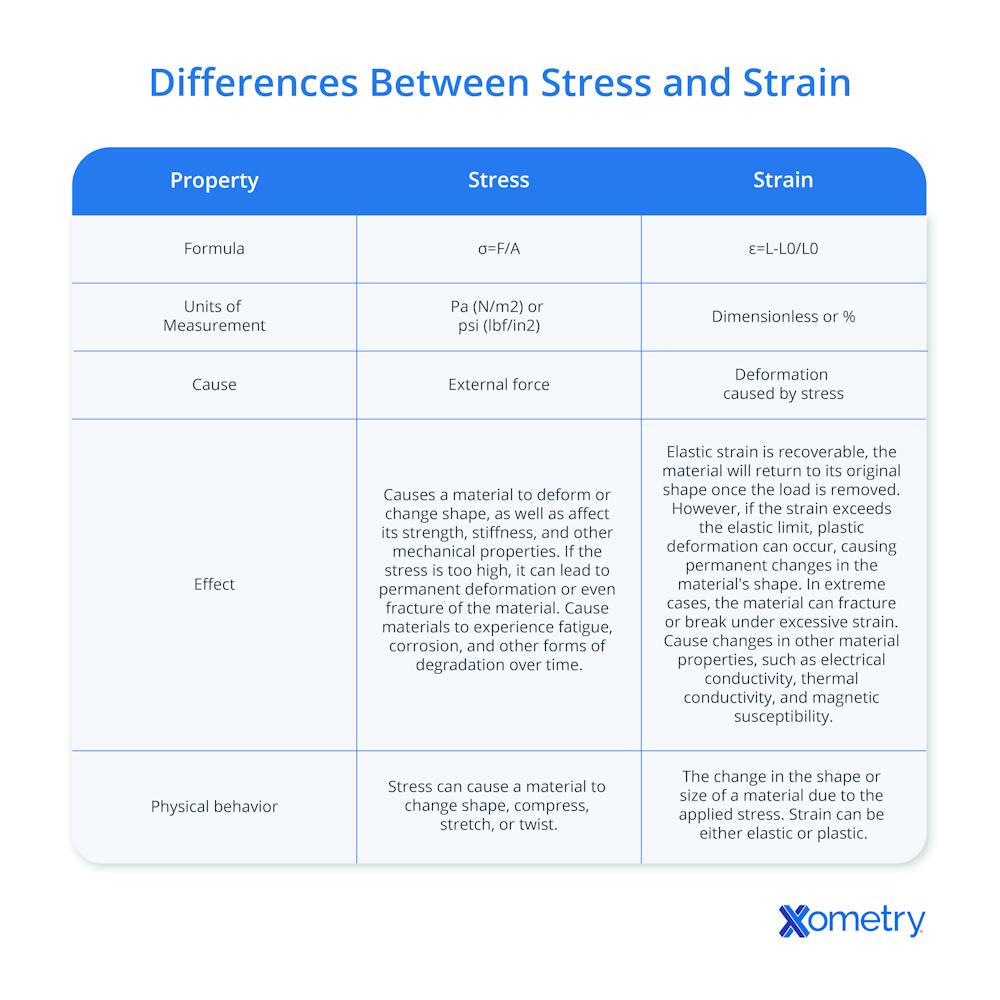
Examples of Stress and Strain of Different Materials
Different materials exhibit different behavior when subjected to stress and strain. Here are some examples of stress and strain of different materials:
- Metals: Ductile metals like stainless steel and many other alloys tend to yield and then deform under stress, while brittle metals such as high-carbon steels are more prone to fracture with minimal plastic deformation. Low-carbon steel, on the other hand, can bend under stress until it reaches a yield point where it becomes strain hardened. This makes it less ductile and more brittle, which can increase the likelihood of failure under certain conditions.
- Polymers: The stress-strain behavior of polymers is diverse.
The red curve represents a brittle polymer, which fractures after only elastic deformation. On the other hand, the blue curve depicts a plastic polymer, with a yield point and a peak stress value. When pulled further, fracture occurs, and the stress value at that point is known as the tensile strength. Elastomers, shown in green, are a unique class of polymers with rubber-like elasticity that can return to their original shape unless extended to the point of fracture.
While stress-strain curves for some polymers may resemble those for metals, polymers have distinct mechanical properties compared to metals or ceramics. For instance, a highly elastic polymer can stretch up to 10 times its original length before breaking, while a metal may only elastically stretch up to 10% of its original length and can stretch plastically to twice its length before fracturing. Moreover, the largest elastic modulus values for polymers are considerably lower than those for ceramics and metals.
How Stress and Strain Relate to Each Other
The simplest way that stress and strain are related to each other is that one causes the other: stress causes strain. The parameter that describes the relationship is Young's modulus. Another way that stress and strain relate is through the material's elastic modulus, which is a measure of the material's stiffness. The elastic modulus relates the stress applied to a material to a resulting strain. The relationship between stress and strain is described by Hooke's law, which states that the stress applied to a material is directly proportional to the strain that results, as long as the material is behaving elastically. This relationship is only valid up until the elastic limit of a material. Mathematically, this can be expressed as:

Where:
- σ is stress
- E is the elastic modulus
- ε is strain
It's important to note that Hooke's law only applies to materials that are behaving elastically. They return to their original shape and size when the stress is removed. If the material is stressed beyond its elastic limit, it will undergo plastic deformation, and Hooke's law no longer applies.
The Stress-Strain Curve
A stress-strain curve is a graphical representation of the relationship between stress and strain in a material. It is obtained by subjecting a sample of a material to gradually increasing levels of stress and measuring the corresponding strain that occurs in the material.
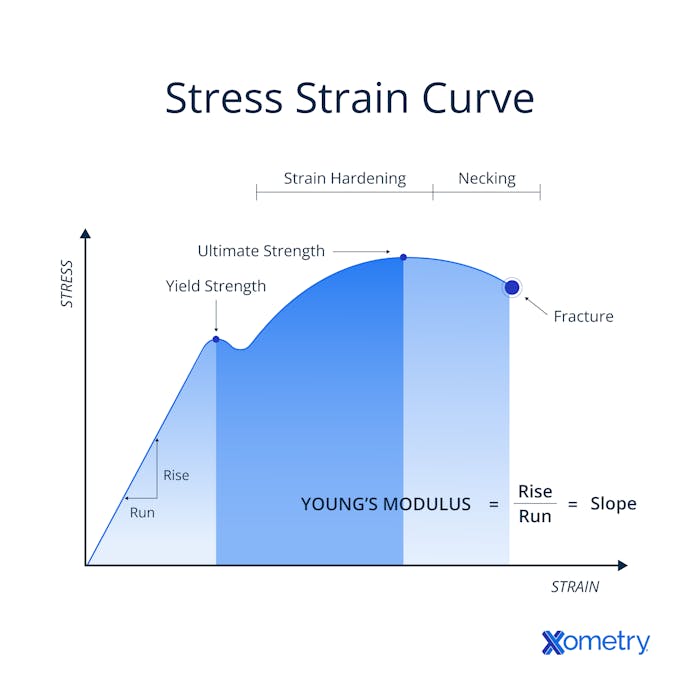
Stress-strain diagrams is commonly used to analyze the behavior of a material throughout its loading until failure. Each material exhibits a unique stress-strain pattern that design engineers can use to extract important mechanical properties such as strength, toughness, elasticity, yield point, strain energy, resilience, and ductility. This information is crucial for designing applications and performing operations like extrusion, rolling, and bending, as it allows for the determination of the forces required to induce plastic deformation.
The stress-strain curve typically has two parts: the elastic region and the plastic region. In the elastic region, the material deforms in response to the applied stress, but the deformation is not permanent. The material returns to its original shape and size when the stress is removed. The relationship between stress and strain in this region is linear, and the slope of the line is called Young's modulus or the elastic modulus of the material.
In the plastic region, the materials’ deformation in response to the applied stress is permanent, meaning that the material does not recover when the stress is removed. The relationship between stress and strain in this region is nonlinear. It depends on the properties of the material, such as its yield strength, ultimate strength, and ductility.
Summary
This article presented stress vs. strain, explained what each is, and discussed their key differences. To learn more about stress vs. strain, contact a Xometry representative.
Xometry provides a wide range of manufacturing capabilities and other value-added services for all of your prototyping and production needs. Visit our website to learn more or to request a free, no-obligation quote.
Disclaimer
The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.


