Stress: Definition, Importance, Types, Examples, and Benefits

Stress is a reaction to a force that acts on a unit area of a material or object. This reaction is internal and when the force exceeds the capacity of the object deformation or failure will occur. That’s where stress analysis comes in.  

Stress analysis is an invaluable tool in the engineering industry. It evaluates how a material will react when placed under different loading conditions. A stress analysis also reveals areas where a structure or object might be susceptible to failure. Therefore, it allows engineers to make design choices to withstand these weaknesses. Stress-strain curves are used to extract all the necessary information that engineers need to ensure that structures and objects are safe and can withstand the forces that will act on them. 

In this article we will be taking a look at stress in materials, the different types of stresses that can develop, and the effects of stress on materials. We will touch a bit on stress analysis and its importance in fields like the engineering services industry. 

What Is Stress in Mechanics?

Stress is defined as the force per unit area that acts on a material. It is used to define how different materials behave under a variety of loading conditions. There are many types of stress that can occur including: shear stress, compressive stress, tensile stress, and torsional stress. 

The main symbol used to represent stress in mechanical and materials engineering is the Greek letter sigma (s). Subscripts may be added to denote tensile (𝜎t) and compressive stresses (𝜎c). The Greek letter tau (𝜏) is used to denote shear stress.

How Does Stress in Mechanics Work?

Stress in mechanics work when a material is subjected to an external force, it responds by developing internal stresses that can cause it to deform or even fail. More specifically, the interatomic bonds stretch. Elastic deformation occurs when the interatomic forces stretch, but ultimately retain their original nearest neighbors and bounce beach when the external force is removed. However, plastic deformation on the other hand will result in permanent deformation when the external force is removed. Failure occurs when a material is no longer able to withstand the stress being applied to it and breaks or deforms permanently. If the stress applied to a material exceeds its elastic limit, the material will experience permanent deformation or even fracture. This is known as plastic deformation, and the material will no longer return to its original shape when the stress is removed. The point at which plastic deformation occurs is called the yield point.

What Is the Importance of Stress of Materials?

Stress analysis plays a crucial role in understanding the behavior and performance of materials and structures under various loading conditions. It helps to predict material behavior, allow optimal materials to be selected, ensure structural integrity, and enhance manufacturing processes. By understanding the effects of stress, engineers can design materials and structures that can withstand forces and loads, minimizing potential risks and improving the overall performance, quality, and reliability of systems/products. Figure 1 below is an example of a simulated stress analysis:

What Is the Use of Stress in Mechanics?

Stress analysis is a crucial tool for understanding the behavior and performance of materials and structures under different loading conditions. It has a wide range of practical applications, including designing and analyzing structures such as buildings, bridges, cars, and machines. Essentially stress analysis plays a crucial role in every part that is under significant service stress. By evaluating the stress distribution within a material, engineers can make informed decisions about material selection and design to ensure that the structure is safe, reliable, and performs optimally. 

Stress analysis is also performed to evaluate the mechanical properties of materials, predict failure under different loading conditions, and improve manufacturing processes by identifying stress concentrations that may lead to defects or failures. This is usually the result of poor design choices. The material can also be the source of stress concentrations if it has unexpected inclusions, has experienced localized corrosion such as crevice corrosion, or has the wrong microstructure. By analyzing stress levels and making design changes accordingly, engineers can optimize the manufacturing process and improve the quality and reliability of the finished product.

How Does Stress Measured in Mechanics?

Unfortunately, there is no way to measure stress directly. Instead, we have to measure both the applied forces and the resulting deformations. In this case, it’s necessary to have an understanding of the relationship between the applied forces (stresses) and the resulting deformations (strains).

Stress analysis is a way to evaluate the effect that different forces can have on an object, and can be performed in different ways. This necessary input to the design process is usually accomplished by some combination of analytical mathematical modeling, computational simulations, and the testing of materials and components or structures. The choice of method/instrument depends on the material being tested, the type of stress being measured, and the level of accuracy required. 

What Are the Units of Stress?

The SI unit of stress is pascals (Pa). One pascal is equivalent to one newton per square meter (N/m2). In the US, pounds per square inch (psi) is another common unit of stress. 

Why Is the Stress of Materials Need To Be Measured?

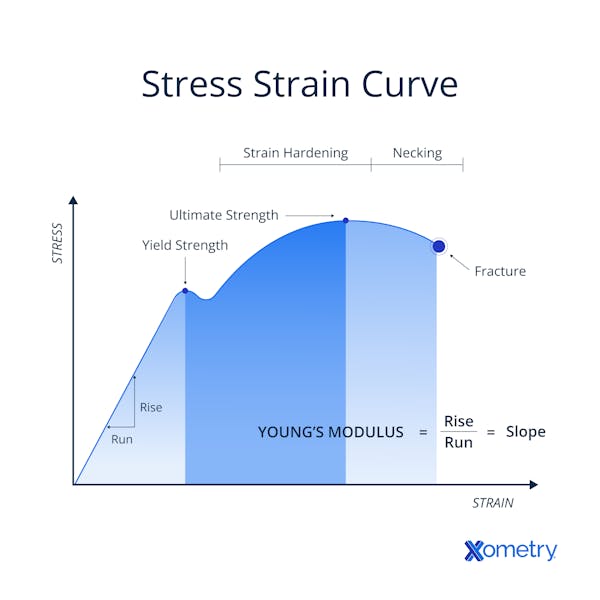
It is very important to measure the capabilities of materials to withstand applied stress because every material has a maximum stress level above which the material will fail. This is called its ultimate strength, which is also known as the tensile strength. This is not to be confused with the yield strength of the material, which is the stress level at which a material begins to deform plastically (i.e., it no longer returns to its original shape when the stress is removed). In other words, it is the stress level at which a material undergoes significant and permanent deformation. The yield strength is typically determined by the stress-strain curve of the material, which shows how the material responds to stress under increasing deformation.

It’s important to know what these values are to ensure that the stress from external loading never exceeds a material’s yield strength.

What Are the Causes of Stress in Materials?

There are various causes of stress in materials, including:

1. External Forces or Loads: Applied loads cause stresses in materials. At stress levels up to the yield point of the material, the bonds between atoms are stretched but do not break. If the stress is removed, the material returns to its original shape. In this region or elastic behavior, the relationship between stress and strain is linear.Externally applied stresses which surpass the yield point of a material will initiate uniform plastic deformation and strain hardening in a ductile material. If the load is too great, a local region of greater plastic deformation (a "neck") will develop, and the part or structure will inevitably fail completely.
2. Changes in Temperature: Changes in temperature can cause stress in materials if one part of the material is free to expand or contract in response to a temperature change, while another part of it is constrained from moving. Constrained thermal expansion/contraction is a common cause of residual stresses, warping, and potential cracking, especially when the rate of temperature is rapid. 
3. Changes in Humidity or Moisture Content: Materials that are sensitive to moisture, such as wood or paper, can experience stress if they absorb or release moisture too quickly. This can cause the material to swell or shrink, leading to deformation or failure.
4. Exposure to Corrosive or Aggressive Environments: This can cause stress in materials, especially if the material is not resistant to the particular environment. Corrosion can reduce the cross-sectional area of a piece, and since stress is equal to the force divided by the area if the area is smaller, the stress rises. This is a direct effect of corrosion resulting in increased stress from the same applied load. Corrosion can also produce corrosion products in crevices. Stress and crevice corrosion are both localized corrosion mechanisms. They both weaken the material by effectively reducing load-carrying capacity, or increasing stress concentrations, or increasing crack growth rate. 

What Are the Effects of Stress in Materials?

Stresses in materials can have various effects, depending on the type, magnitude, and duration of the stress. Some common effects of stress on materials include:

1. When a material is subjected to stress, it may undergo deformation, which can be either elastic or plastic. Elastic deformation is reversible and disappears when the stress is removed, while plastic deformation is irreversible and can lead to permanent deformation or failure of the material.
2. Stress can cause a material to change its dimensions, which can result in distortion or warping of the material. 
3. Stress can also alter the mechanical properties of a material, such as its strength, stiffness, and toughness.
4. High stress can initiate cracks in a material, which can propagate and ultimately lead to failure. This is especially a concern for materials subjected to cyclic loading or fatigue, as repeated stress cycles can cause cracks to grow and eventually cause failure.
5. The most severe effect that stress can have on materials is failure, which can occur suddenly. 

What Is the Formula of Stress?

The basic formula for stress is given as:

σ = F / A

Where:

• σ is stress, units of Pa or psi
• F is the applied force
• A is the cross-sectional area of the material. 

This formula can change for the different types of stresses. 

How To Calculate Stress?

Stress can be calculated by dividing the applied force by the cross-sectional area of the material under stress. This results in a quantity expressed in units of force per unit area, such as psi or Pa.

This formula can change for the different types of stress: true stress and engineering stress. True stress is the ratio of the applied load to the actual cross-sectional area of the material at any given point in time whereas engineering stress is the ratio of the applied load to the original cross-sectional area of a material. In general, engineering stress is easier to measure and calculate than true stress and is often used in engineering applications. However, true stress is more accurate and takes into account the actual deformation that a material undergoes under load.

What Are the Different Types of Stress in Mechanics?

There are different types of stresses that can act on a material, object, or structure. These stresses are listed and discussed in the sections that follow. 

1. Shear Stress

Shear stress, or tangential stress, is the stress that results when a material is subjected to opposing forces that act parallel to each other, but in opposite directions. The formula for calculating shear stress is given by the equation:

𝜏 = F/A

Where:

• τ is the shear stress
• F is the force applied
• A is the area over which the force is applied

Shear stress is a tensor quantity. This means that the direction is also involved along with magnitude.

2. Tensile Stress

Tensile stress is a measure of the internal forces that are acting on a material when it is subjected to an external load or force that tries to pull it apart or elongate it. Tensile stress is defined as the amount of force per unit area of the cross-sectional area that is applied to a material to cause it to elongate or stretch. It is calculated by dividing the applied force (or load) by the cross-sectional area of the material that is perpendicular to the direction of the load.

Tensile stress is an important factor to consider in many engineering applications, as it can cause materials to elongate or even fail if the stress exceeds the material's yield strength or ultimate strength. 

3. Bending Stress

Bending stress is the stress that results from the application of a bending moment to a material, causing it to deform. This results in the development of a combination of tensile and compressive stresses through the cross-section of the material and creates a stress gradient that causes the material to bend. Figure 2 is an illustration of bending stress:

The formula for bending stress is given by:

σb = - (My)/I

Where:

• σb is the bending stress
• M is the bending moment
• y is the distance from the neutral axis to the point where the stress is being calculated
• I is the second moment of area

4. Torsional Stress

Torsional stress occurs when a material is subjected to a twisting or rotational force. When a material is subjected to torsion, the individual layers of the material will deform and twist relative to one another, leading to shear stresses within the material.

The formula for calculating torsional stress is: 

τ = T*r/J

Where:

• τ is the torsional stress
• T is the applied torque
• r is the radius of the material or distance from the center point of the area of the cross-section
• J is the polar moment of inertia of the cross-section

5. Compressive Stress

Compressive stress is created by subjecting a material to a force that acts perpendicular to its cross-sectional area, causing the material to shorten in the direction of the force, but it thickens normally in the direction of the force. This may result in a small decrease in the volume of the material and an increase in its density.

The formula for compressive stress is:

σc = F / A

Where: 

• σc is the compressive stress
• F is the compressive force
• A is the cross-sectional area of the material

6. Longitudinal Stress

When a material is subjected to an axial load, such as tension or compression, it experiences a change in length along its longitudinal axis. The material will either elongate or shorten, depending on the direction of the load. This change in length leads to the development of longitudinal stress within the material. This type of stress is commonly observed in rods or bars that are subjected to axial loads.

7. Volumetric Stress

It is referred to as bulk stress or volumetric stress when the applied or deforming force affects an object in all three dimensions, changing its volume. It occurs when a body's volume changes as a result of a deforming force.

Volumetric stress is important in a variety of applications, such as in the analysis of fluids and solids under pressure, and in the design of pressure vessels and hydraulic systems.

8. Normal Stress

Normal stress, also known as axial stress, is the stress that develops when a force is applied perpendicular to the surface of an object. It can either be compressive stress or tensile stress, depending on whether the force is pushing or pulling on the object.

The formula for normal stress is:

σ = F / A

Where:

• σ is the normal stress
• F is the applied force
• A is the cross-sectional area of the object

9. Fatigue Stress 

Fatigue is a phenomenon that occurs in materials subjected to cyclic stresses and strains at high-stress concentration locations. This leads to a process of progressive localized plastic deformation. This process can eventually result in cracks or complete fractures after a sufficient number of fluctuations. In other words, fatigue can lead to the failure of a material due to the repeated application of stress and strain, even when the maximum stress level is below the material's yield stress. Fatigue stress is a common cause of failure in many engineering applications, including aerospace, automotive, and structural components. 

What Are Examples of Materials That Are Used in Engineering, and How Do They Handle Stress?

Here are five examples of materials used in engineering and how they respond to stress:

1. Steel: A common material used in construction and engineering due to its high strength, and toughness. It can handle both tension and compression stresses well, making it suitable for use in beams, columns, and other structural components.
2. Aluminum: A lightweight material that is also strong and corrosion-resistant. It can handle loading in both tension and compression, making it useful in applications such as aircraft wings and automotive parts.
3. Concrete: A composite material made up of cement, sand, and aggregate. It is strong in compression but weak in tension, so it is often reinforced with steel to increase its tensile strength. Concrete is commonly used in building foundations, walls, and bridges.
4. Plastics:a versatile group of materials that can be molded into different shapes and sizes. They are lightweight and have good resistance to chemicals and corrosion. Different types of plastics can handle different types of stress, such as polyethylene, which is good at handling impact stress, and polycarbonate, which is good at handling bending stress.
5. Titanium: A lightweight and strong material that is resistant to corrosion. It is often used in aerospace and biomedical applications due to its high strength-to-weight ratio and biocompatibility. 

What Are Examples of Materials Are Used in 3D Printing, and How Do They Handle Stress?

Here are five examples of materials used in 3D printing and how they respond to stress:

1. PLA (Polylactic Acid): PLA is a biodegradable thermoplastic made from renewable resources such as corn starch or sugarcane. It is relatively low-cost, easy to print, and can handle low-stress applications such as prototyping, figurines, and educational models.
2. ABS (Acrylonitrile Butadiene Styrene): ABS is a tough, impact-resistant thermoplastic used in a variety of applications, such as automotive parts, toys, and electronic housings. It can handle moderate stress, including impact, compression, and tension.
3. Nylon: Nylon is a strong, durable, and flexible thermoplastic commonly used in applications that require wear resistance and flexibility, such as gears, hinges, and textiles. It can handle high-stress applications and has a high strength-to-weight ratio.
4. PET (Polyethylene Terephthalate): PET is a commonly used thermoplastic in 3D printing that is strong, lightweight, and resistant to impact and chemicals. It is often used in applications such as water bottles, packaging, and medical devices.
5. TPU (Thermoplastic Polyurethane): TPU is a flexible and elastic thermoplastic commonly used in applications that require shock absorption and vibration dampening, such as phone cases, footwear, and sporting equipment. It can handle low to moderate stress and has good tensile strength and elongation properties.

What Are the Benefits of Stress in Materials?

Some of the key benefits of stress analysis in materials include:

1. Can predict how materials will behave under different loading conditions. This information is crucial for designing materials and structures that can withstand the forces and loads they are subjected to, minimizing potential risks.
2. Help identify areas of high stress that may be prone to failure and make design changes accordingly.
3. Optimizes the properties of materials, such as their strength, ductility, and toughness, by providing a means to compare the performance of different potential material formulations.
4. Identifies potential problems before they occur, leading to cost savings by preventing failures, reducing the need for repairs, and minimizing downtime.

What Are the Limitations of Stress in Materials?

While stress analysis is an essential tool for understanding material behavior and designing safe and reliable structures, there are several limitations to its application:

1. Often relies on simplified assumptions about material behavior and loading conditions, which may not accurately reflect the complexity of real-world scenarios. These simplifications can lead to errors and inaccuracies in stress predictions.
2. The behavior of materials can vary significantly due to factors such as manufacturing variability, environmental conditions, and aging. Stress analysis may not account for these variations, leading to inaccurate predictions of material behavior.
3. The loading conditions on a structure or component may be too complex to accurately predict using stress analysis alone. In these cases, finite element analysis, which is a more evolved type of stress analysis, may be necessary to accurately model the behavior of the structure.
4. A company can be analysis-resource constrained, so engineers have to consider the application of the most computationally intensive techniques with care.
5. Designers typically use safety factors to account for the uncertainties and limitations of stress analysis. However, these safety factors can sometimes lead to overdesign, resulting in unnecessary costs or weight in the final structure. It could also increase the environmental impact. 

What Are Some Stress-Related Failure Modes?

The type of failure can be different depending on the material or the stress that was applied. Some of the most common failure modes are listed below:

1. Fracture Failure: Fracture failure can be caused by a number of different mechanisms. It refers to the complete breakage of the component or structure, as opposed to failure through excessive plastic deformation, for example, where the parts may still be connected. 
2. Buckling Failure: Buckling failure occurs when a structure is subjected to a compressive force that causes it to bend or buckle, resulting in structural failure.
3. Creep Failure: Creep failure occurs when a material is subjected to a constant load over a long period, causing it to slowly deform and eventually fail.
4. Deflection Failure: This is a type of failure that occurs when a component or structure deflects beyond its capacity to return to its original position, leading to permanent deformation or collapse. This can occur due to excessive loading or inadequate stiffness of the component or structure.
5. Tensile Failure: Tensile failure occurs when a material is subjected to a pulling force that exceeds its tensile strength, causing it to fracture.
6. Compressive Failure: This type of failure occurs when a material is subjected to a compressive force that exceeds its compressive strength, causing it to buckle or collapse.
7. Shear Failure: This occurs when a material is subjected to a shear force that exceeds its shear strength, causing it to fracture or break.

It is possible for more than one failure mode to occur at the same time. Other types of failures that are also common can be due to factors like corrosion, wear, erosion, and distortion.  

How Is the Stress-Strain Relationship Significant in Mechanics?

Stress and strain are closely linked properties. Stress refers to the force that is applied to a material or object, divided by its cross-section. Strain is the deformation or displacement that results from the applied force. Knowing the values of a material's yield and tensile stress, as well as its elongation, a measure of the strain it can tolerate, can be valuable for determining whether the component or material will be able to withstand various loading conditions.

A stress-strain diagram for a material being considered for use in an application is an invaluable tool. It tells engineers how much force a given cross-section of material can withstand before permanent deformation or failure occurs. Also, by subjecting materials to different levels of stress and measuring the resulting strain, engineers can determine the material's properties, including its strength, stiffness, and ductility. 

What Is the Difference Between Tensile Stress and Compressive Stress?

Tensile stresses develop within a material when it is stretched, and the atoms of the material try to move further apart. Compressive stresses develop when a material is pressed on, and the atoms must either move closer together or move out of the way depending on the level of force applied.

Ultimate tensile strength is the highest stress that a material can withstand before the onset of unstable plastic deformation, leading to failure. Compressive strength is similar but is the stress that can be accommodated before the material buckles. 

What Is the Difference Between Normal Stress and Shear Stress?

The difference between normal stress and shear stress is this: normal stress occurs when a force is applied perpendicular to the surface of the object, whereas shear stress is when the force is applied parallel to the surface. 

Summary

This article presented stress, explained what it is, and discussed its importance and benefits. To learn more about stress, contact a Xometry representative.

Xometry provides a wide range of manufacturing capabilities and other value-added services for all of your prototyping and production needs. Visit our website to learn more or to request a free, no-obligation quote.

Disclaimer

The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.