Elastic Modulus: Definition, Values, and Examples

Elastic modulus, often referred to as Young's modulus, is a measure of a material's stiffness or resistance to elastic (non-permanent) deformation under stress. This property is essential in engineering and materials science, as it determines a material's ability to support loads and maintain its shape. Elastic modulus is expressed as stress (force per unit area) with units of pascals (Pa) or pounds per square inch (psi). Elastic modulus is determined by calculating the slope of the elastic portion of the stress-strain curve. The elastic modulus varies significantly across materials, depending on their atomic structure and bonding. Stiffer materials have a higher elastic modulus.

This article provides an overview of the elastic modulus, its measurement, units, and examples of materials with varying values.

What Is Elastic Modulus?

Elastic modulus is defined as the ratio of stress to strain in the linear (elastic) region of a material’s deformation, representing its stiffness or resistance to elastic deformation. It is a measure of a material’s rigidity or stiffness. The modulus of elasticity, in terms of the stress-strain curve, is the slope of the stress-strain curve in the region of elastic behavior, where stress is linearly proportional to strain. Young’s modulus, also known as the tensile modulus or modulus of elasticity in tension, is one specific type of elastic modulus. Other types include shear modulus and bulk modulus.

What Is the SI Unit of Elastic Modulus?

The modulus of elasticity is measured in pascals (Pa), the same SI unit used for stress. MPa and GPa are usually used to express the modulus of elasticity because of the large magnitude of typical values.

What Is an Example of Elastic Modulus?

Steel is a common material used in construction due to its strength and durability. Its high elastic modulus of approximately 200–210 GPa indicates that it is very stiff and resists elastic deformation under applied stress, making it ideal for use in structures such as buildings and bridges. This property allows the steel to resist elastic bending under load, though it may still yield or fail under excessive stress. In addition, steel's high elastic modulus makes it an excellent choice for use in machine parts and tools, where stiffness and resistance to bending are essential factors. Its stiffness ensures dimensional stability, which helps machines produce precise parts with minimal deflection or compliance under load. A high elastic modulus does not necessarily imply brittleness; steel, for example, is both stiff and ductile depending on its alloy composition and heat treatment. It is recommended to consider the specific application and potential stresses that steel will be subjected to in order to ensure its safe and effective use.

What Are the Elastic Modulus Values?

The elastic moduli for some common materials are listed in Table 1 below:

How Are the Values of Elastic Modulus Expressed?

The value of elastic modulus is typically expressed in units of pressure, such as pascals (Pa) in the SI system or pounds per square inch (psi) in the Imperial system. It is a measure of a material's stiffness or resistance to elastic deformation under stress.

There are different types of elastic modulus depending on the type of stress being applied. The most commonly used elastic modulus is Young's modulus. Young’s modulus measures the ratio of stress to strain when stress is applied perpendicular to the material's cross-sectional area.

The formula for Young's modulus is:

Other types of elastic modulus include the bulk modulus and the shear modulus. The bulk modulus measures the resistance to compression, and the shear modulus measures the resistance to deformation under shear stress.

What Material Has the Highest Elastic Modulus?

Diamond has the highest known elastic modulus,  approximately 1050–1200 GPa, and is also considered to be the hardest known material. This is considerably higher than all types of plastics and metals. The elastic modulus of most plastics typically ranges from 1.5 to 5 GPa, depending on the polymer type and formulation.

In contrast, the elastic modulus of metals is generally much higher than that of plastics. The elastic modulus of metals can vary widely depending on the specific material and its composition. Most metals have elastic moduli in the range of 50 to 400 GPa. It's important to note that these are general ranges. The elastic modulus of a specific material can vary depending on factors such as temperature, strain rate, and the presence of defects or impurities.

What Does a Large Elastic Modulus Value Indicate?

A large elastic modulus indicates that a material is very stiff. It means that a high amount of stress results in only a small amount of elastic strain. Elastic modulus is a crucial design parameter when calculating elastic deflections in structural or mechanical components.

What Does a Small Elastic Modulus Value Indicate?

A small elastic modulus indicates that it does not take much force to induce a considerable amount of elastic strain in a material. It is flexible, not stiff. It will deform elastically with minimal applied tensile or compressive stress. Rubber is an example of such a material, with a very low elastic modulus of approximately 0.01 to 0.1 GPa, depending on the specific type and testing conditions.

What Is the Elastic Modulus Symbol?

The symbol for elastic modulus is E, and it represents Young’s modulus, the most common type of elastic modulus. It is defined as the ratio of stress to strain within the linear (elastic) region of the stress-strain curve. Elastic modulus is measured in pascals (Pa) or pounds per square inch (psi).

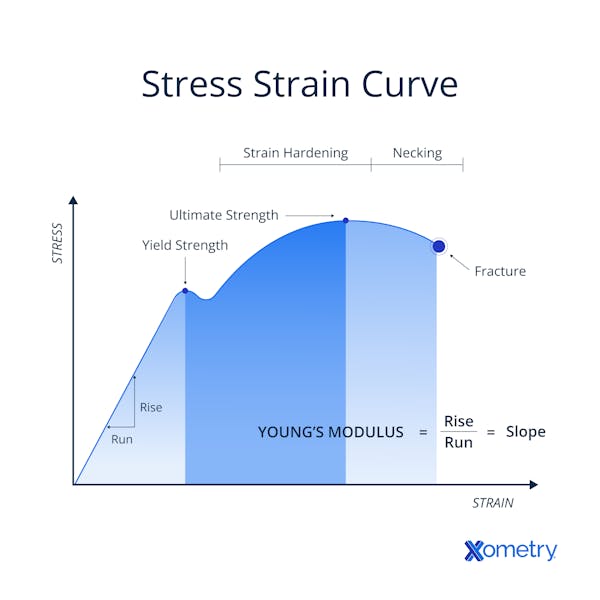
How Is Elastic Modulus Determined?

The elastic modulus of a material is determined by generating a stress-strain curve. The slope of the linear (elastic) portion of this curve is calculated to obtain the modulus. This involves applying a gradually increasing force to a material sample while recording the stress and resulting strain. In the initial linear region, stress and strain are proportional, and their ratio gives the elastic modulus.

What Is the Elastic Modulus Equation?

The equation for elastic modulus (E) is:

E=𝜎/𝜀

Where σ is the applied stress and ε is the resulting strain within the elastic range of the material. The equation for elastic modulus is simply the ratio of the stress applied to a material, to the strain resulting from that stress.

What Is the Difference Between Elastic Modulus and Shear Modulus?

Elastic modulus (Young’s modulus) measures a material’s resistance to deformation under tensile or compressive stress, while shear modulus measures resistance to deformation under shear stress. The main difference is the direction of applied stress: elastic modulus measures resistance to normal (tensile or compressive) stress, while shear modulus measures resistance to shear (parallel) stress.

Summary

This article presented elastic modulus, explained what it is, and discussed its importance and how to calculate it. To learn more about elastic modulus, contact a Xometry representative.

Xometry provides a wide range of manufacturing capabilities and other value-added services for all of your prototyping and production needs. Visit our website to learn more or to request a free, no-obligation quote.

Disclaimer

The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.