The proportional limit is a crucial point on the stress-strain curve that marks the transition from linear to nonlinear behavior in the stress-strain relationship. It denotes the highest stress at which the material will still respond in a way that is proportional to the applied strain. Beyond this point, the material no longer obeys Hooke's Law, and the stress-strain relationship becomes nonlinear. Understanding the behavior of materials under mechanical stress requires a fundamental understanding of the proportional limit concept.
Several criteria must remain true if we are to say that a material remains under the proportional limit. It must show a linear stress-strain relationship, cannot exhibit necking or localized deformation, and must not experience permanent deformation. The proportional limit plays a significant role in determining a material's mechanical properties because it tells engineers about the material's elastic behavior so they can design safe and effective structures. This article will discuss the proportional limit concept, its essential features, and other topics.
What Is a Proportional Limit?
The proportional limit defines the uppermost level of stress at which a material can retain its elastic behavior. A stress-strain graph illustrates where the relationship between stress and strain remains linear. The gradient of the stress-strain curve in this area defines its elastic modulus, and in this region, the material obeys Hooke's law. The proportional limit establishes the highest stress that a material can endure. It does not necessarily mark the onset of permanent deformation. The material will enter the plastic deformation region (where it will undergo permanent shape changes) if the stress exceeds the elastic limit, which may occur slightly beyond the proportional limit.
Therefore, the proportional limit serves as a crucial parameter for evaluating a material's mechanical properties and its ability to withstand applied loads. It's important to note that an evaluation of the proportional limit may not be explicitly required by many testing standards. Nevertheless, it is often used for educational purposes to demonstrate the linear elastic behavior of materials rather than in practical applications within the materials testing industry.
What Is the Concept of Proportional Limit in Material?
The proportional limit in materials denotes the maximum stress they can withstand while still exhibiting a linear correlation between stress and strain. It marks the end of linear elasticity but does not necessarily coincide with the onset of plastic deformation. The stress and strain are directly proportional to one another until they reach the proportional limit. Beyond this point, the material's stress-strain behavior becomes nonlinear, though it may still be elastic. It is a crucial factor in determining how well a material will perform mechanically and maintain its structural integrity under various loading scenarios. Stress-strain curves from experiments can explicitly demonstrate this limit.
How Is the Proportional Limit Defined in the Context of Stress-Strain Relationships?
The stress-strain relationship describes how a material responds to applied forces, specifically in terms of the resulting stress (force per unit area) and strain (deformation per unit length). A stress-strain curve, which plots stress on the y-axis and strain on the x-axis, is used to represent it graphically. The proportional limit is an important location on this stress-strain curve. It represents the maximum stress that a material can experience and still maintain a linear relationship between stress and strain, in accordance with Hooke’s law.
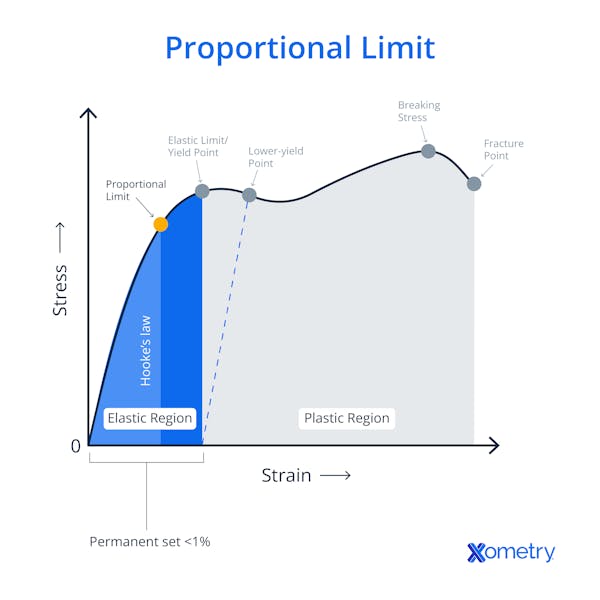
Below the proportional limit, the stress-strain curve forms a linear relationship, indicating purely elastic deformation. Beyond this limit, the stress-strain relationship becomes nonlinear, though the material may still deform elastically until it reaches the elastic limit. To determine the proportional limit on a stress-strain graph, you calculate the slope of the linear portion of the curve, dividing stress by strain. The point where this slope starts deviating from linearity corresponds to the proportional limit.
What Are the Key Characteristics of the Proportional Limit in Materials?
The key characteristics of the proportional limit include:
- Maximum Stress: The proportional limit represents the highest stress level that a material exhibits a linear relationship between stress and strain.
- Linear Relationship: Below the proportional limit, stress and strain exhibit a linear relationship. The material deforms elastically, and the deformation is reversible.
- Elastic Behavior: The material returns to its original shape after the applied stress is removed, as long as it doesn’t surpass the proportional limit.
- Plastic Deformation Threshold: Exceeding the proportional limit leads to nonlinear behavior, but not necessarily plastic deformation.
- Structural Integrity Indicator: The proportional limit provides important information for assessing the material's mechanical behavior and structural integrity under various loading conditions.
How Does the Proportional Limit Affect the Behavior of a Material Under Stress?
The proportional limit significantly influences the behavior of a material under stress. Below the proportional limit, it will act in an elastic manner. It deforms temporarily and returns to its original shape when the stress is released. The stress-strain relationship is linear, indicating a direct proportion between stress and strain.
However, once the proportional limit is exceeded, the material enters a nonlinear stress-strain region. Depending on the material, this may still be elastic deformation or may progress to plastic deformation. This means that even after the stress is removed, the material may or may not fully recover its original shape, depending on whether the elastic limit is also exceeded. The proportional limit serves as an indicator of the maximum stress a material can sustain while maintaining its linear elastic behavior.
What Is the Significance of the Proportional Limit in Mechanical Properties?
The proportional limit is a critical mechanical property for engineers and designers. It serves as a fundamental parameter for characterizing material behavior under stress and strain. By identifying the proportional limit, engineers and material scientists can determine the maximum stress a material can withstand while still behaving in a linear-elastic manner. This information is crucial when designing structures and components that experience loading conditions.
Moreover, the proportional limit marks the end of linear elasticity but not necessarily the onset of plastic deformation. It provides insights into the material's ductility, stiffness, and resistance to permanent deformation. This knowledge is essential when selecting materials for specific applications, ensuring structural integrity, and mitigating potential failure modes.
How Is the Proportional Limit Determined in an Experiment?
The proportional limit can be determined through a tensile test, a common experimental method used to evaluate the mechanical properties of materials. In this test, a standardized specimen is subjected to gradually increasing tensile forces until it reaches its failure point.
To identify the proportional limit, the stress-strain curve is plotted based on the measured values of stress (force per unit area) and strain (deformation per unit length). The proportional limit is typically identified as the point where the curve starts deviating from linearity. It is often determined by calculating the slope of the initial linear portion of the curve, by using the stress/strain ratio formula, or by detecting the point at which the linear slope begins to deviate.
What Factors Can Influence the Value of the Proportional Limit?
Several factors can influence the value of the proportional limit in materials:
- Material Composition: Different materials have varying inherent strengths, crystal structures, and bonding, affecting their proportional limit.
- Temperature: The temperature at which the material is tested can impact its proportional limit, as thermal energy affects atomic mobility and material behavior.
- Strain Rate: The rate at which the material is deformed can influence its proportional limit. Higher strain rates may lead to changes in deformation mechanisms and alter the limit.
- Alloying Elements: The addition of alloying elements can modify the material's microstructure and strengthening mechanisms, and thus affect the proportional limit.
- Sample Preparation: Variations in sample preparation, such as specimen geometry, surface conditions, and fabrication techniques, can influence the measured values of the proportional limit.
How Does the Proportional Limit Differ From Other Points on the Stress-Strain Curve?
The proportional limit differs from other points on the stress-strain curve, such as the yield point and ultimate strength, in terms of the material behavior and corresponding deformation. The proportional limit is the highest stress point on the stress-strain curve at which the material exhibits purely elastic behavior with a linear relationship between stress and strain. In this region, no plastic (permanent) deformation occurs.
The yield point, on the other hand, denotes the stress at which appreciable plastic deformation starts to occur. It is the point at which the material switches to plastic behavior as the primary deformation mode. The maximum amount of stress that a material can withstand before failing or weakening is referred to as the ultimate strength. The proportional limit occurs in the linear-elastic region, while both the yield point and ultimate strength fall within the plastic region.
For more information, see our guide on the Stress and Strain Curve.
What Are the Implications of Exceeding the Proportional Limit in Terms of Material Failure?
When a material exceeds the proportional limit, it deforms beyond its elastic range. This results in nonlinear deformation, which means that even after the applied stress is removed, the material may not fully return to its original shape. The result is a reduction in the material's capacity to support loads and an increase in its susceptibility to failure because the material's mechanical properties, such as strength and stiffness, are compromised. If loading continues beyond the yield point, deformation behavior may include necking, localized thinning, and eventually fracture. By staying under the proportional limit, your structure will maintain its integrity and won’t reach the point of catastrophic failure.
Can the Proportional Limit be Exceeded Without Causing Creep Deformation?
Yes, the proportional limit can be exceeded without causing creep deformation. The proportional limit is the maximum stress at which a material exhibits linear elastic behavior. Once this limit is surpassed, the material undergoes nonlinear deformation, which may include plastic deformation but does not necessarily lead to creep. Creep is the time-dependent deformation that occurs under a constant load or stress, often observed at elevated temperatures or high levels of stress. For more information, see our guide on Creep Materials.
What Is the Difference Between Proportional Limit and Elastic Limit?
The proportional limit is the maximum stress at which a material exhibits linear elastic behavior, while the elastic limit is the maximum stress beyond which the material undergoes permanent deformation, even after the stress is removed. In many cases, the two limits occur at the same point, but some materials exhibit a small amount of additional elastic deformation that doesn’t follow the ordinary linear stress-strain behavior. The elastic limit is difficult to determine with precision, so it is usually not used for design purposes.
Summary
This article presented proportional limit, explained what it is, and discussed its various characteristics. To learn more about proportional limit, contact a Xometry representative.
Xometry provides a wide range of manufacturing capabilities and other value-added services for all of your prototyping and production needs. Visit our website to learn more or to request a free, no-obligation quote.
Disclaimer
The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.


