A Step-by-Step Guide on How To Calculate Young’s Modulus

Whether you’re fresh out of college or it’s been some time since you’ve taken math classes, it’s always helpful to review equations that frequently show face in the work that you do. One example of this that we’d like to cover in our engineering fundamental series is Young’s modulus, which we’ll define below and then break down how to calculate it.

To calculate Young’s modulus of elasticity, follow these steps:

1. Determine the Initial Length of the Substance Using a Micrometer

In the first step of the process, the initial length of the material or item must be measured using a micrometer. This crucial measurement serves as a baseline reference point for all subsequent calculations. Only when we have an accurate measurement of the original configuration can we properly assess its deformation and behavior under applied forces. This initial measurement is fundamental when calculating Young's modulus. Engineers and scientists can make well-informed decisions regarding the materials and structural design if they have a precise starting point that lays the groundwork for trustworthy and meaningful results.

2. Use the Same Micrometer to Determine the Material's Cross-Sectional Area

While the material's length marks the first measurement, the same micrometer should be used to assess its cross-sectional area. Carefully measure both its width and height so you can accurately calculate all subsequent changes. Since the cross-sectional area directly impacts the material's response to applied forces, it plays a vital role in determining Young's modulus. This precise assessment allows for a comprehensive evaluation of the material's stiffness and its ability to withstand deformation. Engineers can design structurally sound and efficient systems based on this valuable information.

3. Measure the Different Diameters of the Substance Using the Micrometer

The next step is to use the micrometer to gauge the item’s various diameters, making sure to take readings at multiple locations. This meticulous approach creates an accurate baseline for subsequent calculations by accounting for any irregularities in the material's dimensions. Precise diameter measurements are essential to calculate Young’s modulus because they tell you the original cross-sectional area of the substance.

4. Apply Forces on the Substance by Using Various Slotted Masses

Engineers next exert forces on the material using a variety of slotted masses to create controlled tension and deformation. They can see and examine how the material responds to various loads during this process. This step evaluates the material's elasticity and ability to effectively withstand external forces, which is important for calculating Young's modulus. Engineers can create dependable and long-lasting structures because the data gathered from these experiments tell them whether a given material will meet the structure’s needs. 

5. Use a Vernier Scale To Measure the Length As the Substance's Components Extend to Different Lengths

Use a Vernier scale to ascertain the substance's elongation during tensile testing precisely. Align the scale parallel to the specimen and take precise readings at regular intervals. The Vernier scale will let you measure deformation accurately enough to calculate Young's modulus. That precision guarantees more dependable Young's modulus values, enhancing the validity of your findings.

6. Graph the Length Measurements Against the Applied Forces

This visual representation of the relationship between stress and strain is crucial for determining Young's modulus. The graph helps you verify and analyze experimental data. The whole process gives you a quantitative measure of the material's stiffness, making it an essential aspect of the calculation process.

7. Calculate Young's Modulus Using the Equation E = Tensile Stress / Tensile Strain = (FL) / (A * change in L)

Young's modulus (E) is the material's stiffness. It’s determined by dividing the tensile stress (F/A) by the tensile strain (ΔL/L₀). This quantification of the material's resistance to deformation is essential for engineers and materials scientists. It aids in material selection, part design, and prediction of behavior. 

What Is Young's Modulus?

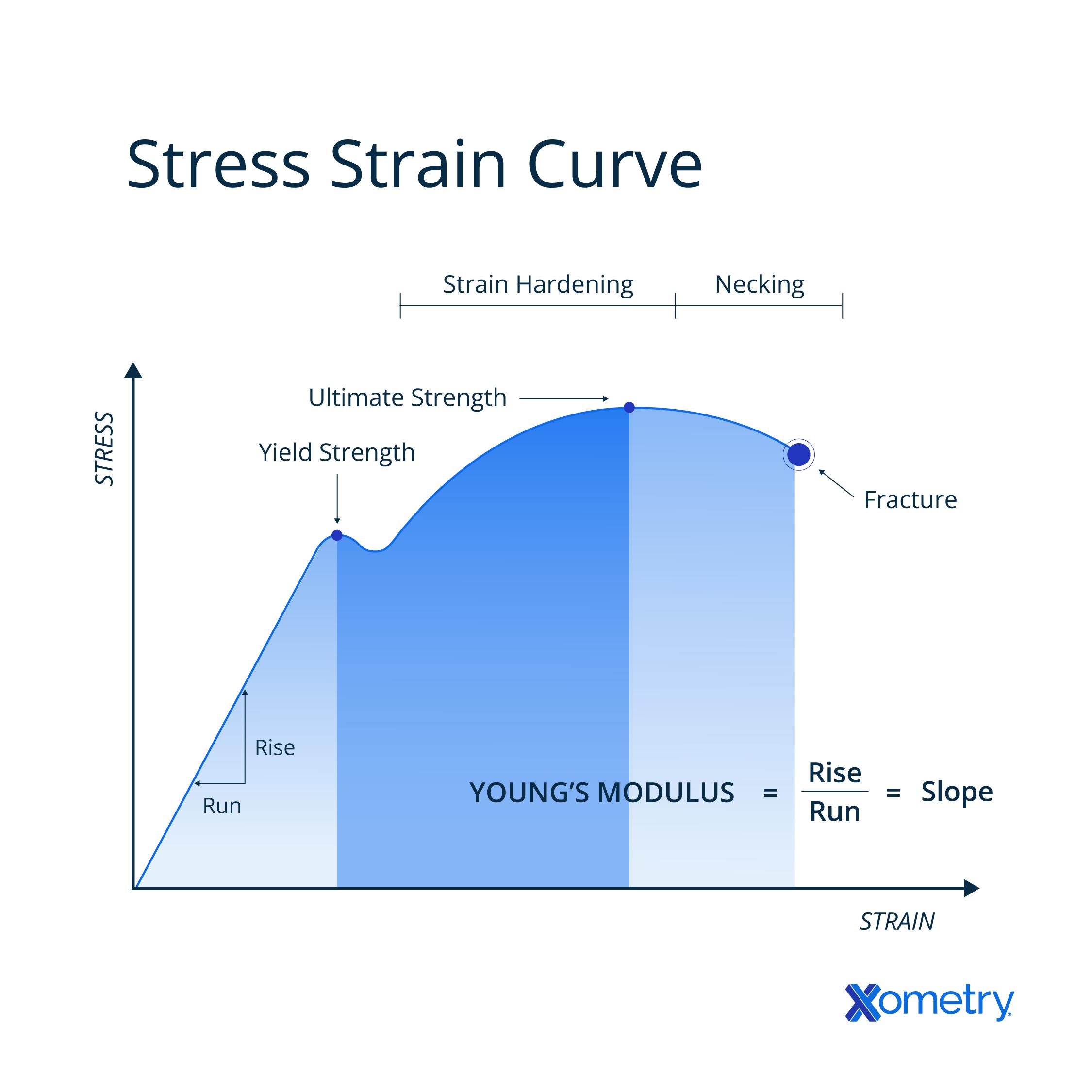
Young’s modulus points to the slope of a stress strain curve and can help show when a material is simply stretching and holding up okay under stress versus when it’s bound to deform or break. It’s an essential insight into the behavior of a material, and can help determine which materials are best to use based on this number and other factors. 

While it’s a common equation found in engineering, you’ll also find it in medical, scientific, and aerospace settings, as knowing this can be the difference between broken parts, implants, and surfaces and ones that stay together. Sometimes you’ll hear team members or fellow coworkers call Young’s modulus the modulus of elasticity.

As you can see in this image, this style of graph can help show Young’s modulus, the ultimate strength point of a material, and at what point you can expect deformation or breakage to occur.

How Does Young's Modulus Work?

Young's modulus is a material property that measures the stiffness and elasticity of a material. When a metal bar is subjected to a force "F" at each end, it deforms, resulting in a change from its original length "L0" to a new length "Ln." Stress is the force "F" divided by the cross-sectional area "A," while a strain is the relative deformation, (Ln - L0) / L0. Young's modulus is then given by (F × L0) / (A × (Ln - L0)), representing the material's resistance to deformation.

Why Is Young's Modulus Important?

Young's modulus is important because it allows engineers to predict when a structural implant will deform. They can thus design the implant to withstand any reasonable stresses it might encounter. Additionally, Young's modulus enables the calculation of dimensional changes in isotropic elastic materials under tensile or compressive loads. This property is valuable in materials science and engineering, ensuring that materials and structures can withstand stress and maintain their integrity.

What Is an Example of Young's Modulus Calculation?

To really help this concept stick, take a look at the following calculations that find the elasticity modulus of different materials:

1. Steel

In this example, we’ll look at a steel rod and find Young’s modulus for it. Consider the equation if the following factors are true:

• The rod has an original length (L0) of 2 meters
• It has a final length (Ln) of 2.04 meters
• The cross-sectional area (A) is 1 square centimeter (0.0001 square meters)
• To get the elongation you’ll subtract L0 from Ln (which will be 4 cm in this case)
• The force (F) applied is 1,000 Newtons (N)

Here’s how you would calculate this: 

Equation: Young’s modulus = (F x L0) / (A x (Ln - L0))

With numbers inputted: Young’s modulus = (1,000 N x 2 m) / (0.0001 m2 x 0.04 m)

Answer: Young’s modulus ≈ 5 x 108 Pascal (Pa)

2. Aluminum

If you’d like to calculate the same equation but with an aluminum rod, here’s how to do so using sample numbers and with less force:

• The rod has an original length (L0) of 2 meters
• It has a final length (Ln) of 2.04 meters
• The cross sectional area (A) is 1 square centimeter (0.0001 square meters)
• To get the elongation you’ll subtract L0 from Ln (which will be 4 cm)
• The force (F) applied is 800 Newtons (N)

Here’s how you would calculate this: 

Equation: Young’s modulus = (F x L0) / (A x (Ln - L0))

With numbers inputted: Young’s modulus = (800 N x 2 m) / (0.0001 m2 x 0.04 m)

Answer: Young’s modulus ≈ 4 x 108 Pascal (Pa)

3. Rubber

Here is how this calculation could be determined if we use a rubber band and possible measurements for this type of material: 

• The rubber band has an L0 of 10 centimeters
• It has an Ln of 15 centimeters
• The cross-sectional area (A) is 1 square centimeter (0.0001 square meters)
• The elongation is 5 centimeters (Ln-L0)
• The force applied is 20 Newtons

Here’s how you would calculate this: 

Equation: Young’s modulus = (F x L0) / (A x (Ln - L0))

With numbers inputted: Young’s modulus = (20 N x 0.1 m) / (0.0001 m2 x 0.05 m)

Answer: Young’s modulus ≈ 4 x 105 Pascal (Pa)

When you compare all of these different materials, you’ll notice that the Young’s moduli for rubber is a much lower magnitude than steel and aluminum, meaning that the former material is more flexible and elastic, whereas the latter materials are stiffer.

What Is Young's Modulus for Steel?

The Young's modulus of steel usually falls between 190 and 215 GPa. This value represents the material's stiffness or ability to resist deformation when subjected to tensile or compressive forces. It is a measure of the material's elasticity, indicating how much it will stretch or compress under stress. Factors such as the: composition, temperature, microstructure, and strain rate of the steel will affect its overall Young’s modulus.

What Is Young's Modulus for Aluminum?

Young's modulus of aluminum is approximately 69 gigapascals (GPa). This value is well established and has been extensively studied in the field of materials science and engineering. Experimental measurements, theoretical calculations, and simulations have consistently confirmed this value. Factors that may affect Young's modulus in aluminum include: temperature, alloy composition, crystal structure, and manufacturing processes. For instance, alloying elements can alter the modulus by affecting the material's intermolecular lattice arrangement and bonding, leading to variations in its mechanical properties.

What Is Young's Modulus for Polyester?

Pure polyester exhibits Young's modulus of around 920 MPa, denoting its stiffness and resistance to deformation under tensile stress. Several factors can impact Young's modulus in polyester, including: its molecular structure, crystallinity, temperature, and manufacturing processes used to create it. Alterations in these aspects may influence the material's elasticity and overall mechanical properties, resulting in fluctuations in the modulus value.

What Are the Benefits of Calculating Young's Modulus?

Engineers use this equation in real-world scenarios for several reasons: 

1. Understanding materials: Knowing the Young’s modulus for a certain material will help you get to know it better and help predict what environments and situations it can be put through with success.
2. Design considerations: When a structure is relying on a specific material or a human needs a particular implant, calculating Young’s modulus will help determine which materials to use, as you’ll have a better understanding of which ones can withstand the stresses. 
3. Stress calculation: You’ll need to know Young’s modulus in order to calculate the stress in a material — another vital factor in engineering and design. 
4. Predicting material failure: With the modulus of elasticity, you can have a much better and more accurate prediction of the point at which a material will break or deform for good under pressure. 

Are There Downsides in Calculating Young's Modulus?

No, there are no downsides in calculating Young's modulus other than the destruction of test articles. It is a fundamental and essential property used in engineering and materials sciences. The calculation involves simple stress-strain testing, which is widely accepted and practiced. Moreover, understanding a material's stiffness and deformation behavior is vital for designing safe and reliable structures and predicting material performance under different conditions.

Are Young's Modulus and Elasticity the Same Thing?

No, Young's modulus and elasticity are not the same. Young's modulus measures a material's stiffness within the elastic limit, while elasticity is a broader concept encompassing a material's ability to deform and return to its original shape. Young's modulus is just one measure of elasticity, which includes other properties like shear and bulk modulus.

Disclaimer

The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.