Strain is a key concept in engineering and physics that describes how a material deforms in response to applied stress. The ratio of an object's change in length or shape to its original length or shape is known as strain. In many disciplines, including structural engineering, mechanical engineering, and materials science, an understanding of strain is essential because it determines how a material will behave under load, and enables the design of structures that can withstand the expected service stresses.
When calculating strain, the amount of material deformation is measured. This deformation is usually expressed as a percentage change in the material's length, area, or volume. Engineers identify several types of strain, based on the kind of stress that produces the particular kind of deformation: longitudinal, lateral, shear, and volumetric strain. Many structures, including bridges, vehicles, and aircraft, experience strain as a result of applied stress in the real world. This article will define strain, its types, and their significance, provide calculation techniques for each type, and give examples of practical applications of strain analysis.
What Is Strain in Mechanics?
In mechanics, strain is a dimensionless measure of the deformation that a material experiences in response to an external force or load. It is described as the ratio of the change in the material's length or shape to that of the original. Stress, or the force applied per unit area, is related to strain by the material's stiffness or elasticity. Epsilon (ε), the symbol for strain, can be written as a percentage or a fractional value. A fundamental idea in mechanics, strain is important in the planning and evaluation of mechanical systems and structures.
What Is the Other Term for Strain?
The other word for strain is "deformation", which describes how a material changes in size or shape as a result of the application of a load or force from the outside. In engineering and physics, deformation is commonly used interchangeably with strain and can take many different forms, including stretching, compression, and bending.
How Does Strain in Mechanics Work?
In mechanics, strain is a concept that describes how a material deforms or changes shape as a result of an external force or stress. Strain is measured using strain gauges, which are tools for detecting and quantifying material deformation. The surface of the material being tested is covered with a grid of fine wire or foil. The strain gauge's wire or foil deforms along with the material being measured, resulting in changes in the gauge's electrical resistance. The degree of strain can be calculated by measuring these variations in resistance.
What Is the Importance of Strain in Materials?
Strain in materials is important because it explains how materials deform under stress. Designing structures that can withstand expected loads without failing requires a thorough understanding of a material's strain behavior. Strain is used to evaluate a material’s ductility and allows engineers to calculate how much energy a material or structure can absorb when being deformed.
What Is the Use of Strain in Mechanics?
Engineers use strain as a key parameter to forecast how materials will behave when subjected to loads. Knowledge of the details of strain behavior is essential for the design and analysis of mechanical parts and structures. The main application of strain in mechanics is to comprehend how materials respond to stress. Any time a force is applied to a substance, deformation or a change in shape results. This deformation can be measured in terms of strain.
To ensure that structures can withstand the loads they are intended to carry, engineers use strain measurements to assess the strength and stiffness of materials. Mechanical parts like gears, bearings, and shafts are also designed using stress and strain concepts. Engineers can make sure that these parts are sturdy enough to withstand the stresses they will experience during operation by measuring the strain imposed on them by particular levels of stress.
How is Strain Measured in Mechanics?
Strain gauges and extensometers are the most common methods used to measure both elastic and plastic deformation. Extensometers directly measure a material's change in length, as opposed to strain gauges, which convert mechanical deformation into an electrical signal. Optical methods, such as digital image correlation, can also be used to measure strain by analyzing images of the material under stress.
What Are the Units of Strain?
The quantity of strain has no dimensions, so it has no units. However, strain is usually expressed as a fractional or percentage change in length. Length changes involved in strain calculations may be measured in meters, millimeters, or micrometers, but strain itself remains unitless.
Why Does the Strain in Materials Need To Be Measured?
When designing structures that can withstand expected loads, it's important to understand how materials behave mechanically under stress. Structures deform under stress, whether elastically (temporarily) or plastically (permanently). Measurements of strain can also reveal details of material characteristics, such as elasticity, plasticity, and fracture toughness, which are essential for choosing the right materials for engineering applications.
What Are the Different Causes of Strain in Materials?
There are many causes of strain in materials, including:
- Mechanical Stress: Mechanical stress is the most common cause of strain in materials. When a force is applied to a material, it undergoes deformation, or strain, which can be either elastic or plastic.
- Electromagnetic Fields: Certain materials, such as magnetostrictive or piezoelectric materials, can experience strain when exposed to electromagnetic fields due to internal interactions between magnetic or electric fields and their crystal structures.
- Radiation: When metals are exposed to radiation, they can undergo a process known as radiation hardening. The material may become more brittle but also stronger as a result of this process. As a result, it is less likely to deform under stress, which can result in brittle fractures. The radiation damages the metal's atoms by interacting with them, leading to flaws and dislocations in the lattice structure. This is comparable to other hardening processes like precipitation hardening and work hardening.
- Fatigue: Fatigue is the gradual weakening of a material due to repeated loading and unloading cycles. This can cause strain in the material, leading to failure over time.
- Creep: Creep is the slow deformation of a material over time due to a constant load or stress. This can cause strain in the material, leading to failure over time.
- Manufacturing Processes: Manufacturing processes such as casting, forging, and welding can cause strain on materials due to the high temperatures and stresses involved in these processes.
What Are the Different Effects of Strain on Materials?
Here are a few typical outcomes of material strain:
- Elastic Deformation: When a material is subjected to a small amount of strain, it may exhibit elastic deformation. It will return to its original shape when the stress is removed. The amount of strain is proportional to the stress applied, according to Hooke's Law.
- Plastic Deformation: If the strain applied to a material exceeds a certain threshold, it may undergo plastic deformation. It will remain deformed even when the stress is removed. The material’s capacity to reorganize its atomic configuration without rupturing the interatomic bonds holding it together determines the degree of plastic deformation.
- Fracture: When a material is subjected to a large amount of strain, it may fracture or break. The amount of dislocation pinning, available slip systems, and atomic bonding in the crystal lattice all affect the amount of strain that can be applied before fracture.
- Thermal Expansion: Materials may exhibit expansion or contraction in response to changes in temperature. This is known as thermal expansion and can result in significant strains in some materials.
- Work Hardening: Some materials may become harder and stronger after undergoing plastic deformation. This is known as work hardening or strain hardening and can occur in metals, polymers, and other materials.
What Is the Formula for Strain?
Strain is a unit of measurement for how much a material deforms in response to stress. Strain is calculated as follows:
ε = ΔL / L₀
Where:
- ε represents strain
- ΔL represents the change in length of the material
- L₀ represents the original length of the material
Strain is equal to the change in length divided by the original length. This formula is commonly used to calculate strain in materials, such as metals, polymers, and composites.
How Is Strain Calculated?
The steps in calculating strain (ε) are listed below:
- Measure the initial length (L0) of the object or material for which you want to calculate the strain.
- Measure the final length (Lf) of the object or material after it has been deformed.
- Subtract the initial length from the final length to get the change (the delta) in length:
ΔL = Lf - L0. - Divide the change in length by the initial length: (ΔL) / L0.
- Multiply the result by 100 to get the strain as a percentage: ((ΔL) / L0) x 100.
Here's an example:
Suppose you have a steel wire with an initial length of 10 cm. After stretching it, you measure its length to be 13 cm.
- L0 = 10 cm (initial length)
- Lf = 13 cm (final length)
- Lf - L0 = ΔL = 3 cm (change in length)
- (ΔL) / L0 = 0.3 (strain as a decimal fraction)
- 0.3 x 100 = 30% (strain as a percentage)
So the strain (ε) in this case is 30%.
What Are the Different Types of Strain That Can Occur in Materials?
The various types of strains that can develop in materials are as follows:
1. Normal Strain
Normal strain describes how a solid material responds to a force that is applied perpendicular to its cross-sectional area. It is measured as the ratio of the change in length to the original length of the material. The formula for normal strain is:
ε = ΔL / L₀
Understanding normal strain is crucial for designing and testing materials in various industries. It can help ensure the safety and reliability of structures and products.
2. Tensile Strain
Tensile strain is the amount of deformation that a material undergoes when it is pulled or stretched. It is measured as the ratio of the change in length of the material to its original length. The formula for tensile strain is:
ε = ΔL / L₀
The measurement of tensile strain is important in materials science and engineering, as it helps to determine a material's ductility and elasticity.
3. Shear Strain
Shear strain is a type of strain that occurs when the particles of a material slide past each other in a parallel direction, causing a change in the shape of the material. It is measured as the change in angle between two originally perpendicular lines in the material. The formula for shear strain is given by:
γ = tan θ
Where:
- γ is the shear strain
- θ is the shear angle
Shear strain is used in the design of various structures and mechanical systems.
4. Thermal Strain
Thermal strain refers to the deformation or change in the size of a material due to temperature changes. Thermal expansion can occur under two different circumstances: non-constrained and constrained. When materials are not constrained, they can move freely in all directions, but when they are, certain directions are restricted, which can cause stress, deformation, or failure. When designing materials and structures, engineers must take into account both conditions to make sure they can withstand the stresses and strains brought on by temperature changes. Thermal strain can be measured using strain gauges or interferometry techniques. The formula for calculating thermal strain is:
ε = αΔT
Where:
- α is the coefficient of thermal expansion
- ΔT is the temperature change
Understanding thermal strain is critical in designing and building structures that can withstand temperature variations. Accurate measurement and calculation of thermal strain can help prevent material failure and extend the lifespan of structures.
5. Compressive Strain
Compressive strain is the deformation that takes place in a material when it is subjected to a contracting force. Under compression, the space between the atoms of a material is reduced, causing the material to become compacted. It is measured by comparing the original and deformed lengths of a test specimen or structure under compression. The formula for compressive strain is:
ε = ΔL / L₀
Compressive strain is important in materials science as it helps determine a material's compressive strength and its ability to resist deformation.
6. Residual Strain
The term "residual strain" describes the internal stress that remains in a material after it has been deformed or subjected to external forces. It can be measured using techniques such as X-ray diffraction or neutron diffraction. The formula for calculating residual strain involves measuring the change in lattice spacing due to deformation. An accurate measure of residual strain can help an engineer understand the residual stress state in a structure, providing needed information for avoiding potential failures. It can also provide valuable information for improving manufacturing processes and designing structures with enhanced performance.
7. Volumetric Strain
Volumetric strain is the term for the volume change that occurs in a material as a result of uniformly applied external forces (hydrostatic strain). It is determined by dividing the volume change by the starting volume. The formula for calculating volumetric strain is:
ε = ΔV/V
Where:
- ΔV is the change in volume
- V is the volume
Volumetric strain is important in various fields such as engineering, geology, and materials science. It aids in predicting how materials will react to stress and in designing structures appropriately.
What Are Examples of Materials Used in 3D Printing, and How Do They Handle Strain?
Engineering employs a variety of materials, each of which has particular properties and strain behavior. Here are some examples of material types commonly used in 3D printing, and examples of how they handle strain:
- Steel: Steel is a common engineering material renowned for its ductility and strength. Steel is the perfect material for high-stress applications like construction, bridges, and heavy machinery because it is ductile enough to accommodate some plastic deformation before final failure.
- Aluminum: Aluminum is frequently used to take advantage of its light weight and corrosion resistance. Aluminum has a high strength-to-weight ratio and adequate ductility for the kinds of construction, automotive, and aerospace applications that demand consideration of the weight of the structure.
- Concrete: Concrete is a widely used construction material due to its strength and durability. Although it has a low tensile strength, concrete can handle high compressive loads. Reinforcing materials, such as steel, are added to concrete to increase its tensile strength.
- Plastics: Plastics are suitable for a variety of applications because they are lightweight and simple to manufacture. They can withstand mild amounts of strain and have good ductility. Plastics are not suited for high-stress applications due to their low strength in comparison to other materials.
- Ceramics: Ceramics are strong and tough materials that work well in applications where high temperatures and wear resistance are necessary. Ceramics are susceptible to failure under stress because they are brittle and have low ductility.
What Are Examples of Polymer Materials Used in 3D Printing, and How Do They Handle Strain?
Here are five polymer materials commonly used in 3D printing and their strain-handling characteristics:
- PLA (Polylactic Acid): 3D printing often uses PLA, a biodegradable and environmentally friendly material. Its moderate tensile strength and relatively high brittleness make it easily breakable when put under stress.
- ABS (Acrylonitrile Butadiene Styrene): A common material for 3D printing, ABS is a solid and durable plastic. It can withstand moderate strain without breaking because of its relatively high tensile strength.
- Nylon: A popular material for 3D printing that is both durable and flexible is nylon. It has the highest tensile strength of the polymers mentioned here. When nylon is subjected to strain, it exhibits high elasticity and toughness, meaning that it can stretch without breaking and can absorb significant amounts of energy before failing.
- PETG (Polyethylene Terephthalate Glycol): PETG is a sturdy and durable material that is widely utilized in 3D printing. It has a moderate tensile strength and can withstand moderate levels of strain without breaking.
- TPU (Thermoplastic Polyurethane): TPU is a versatile and elastic material that can be utilized in 3D printing. Although it has a low tensile strength, its elastic properties allow it to withstand large amounts of strain without cracking.
For more information, see our 3D printer guide.
How Does Strain Relate to Stress?
Strain is the result of the material's deformation or changes in shape as a result of forces that were applied to it. The elastic modulus of the material describes the relationship between stress and strain. Strain is a measure of deformation, whereas stress is a measure of force per unit area.
What Comes First, Stress or Strain?
When a material sample is subjected to a force, stress comes first, then strain follows. Stress is defined as the force per unit area applied to an object, whereas strain is the resultant deformation of the object. Stress is the cause, and strain is the effect of stress on the material.
What Is the Stress-Strain Curve?
A stress-strain curve illustrates how a material responds to an applied force. Figure 1 below is an example of a tensile stress-strain curve:
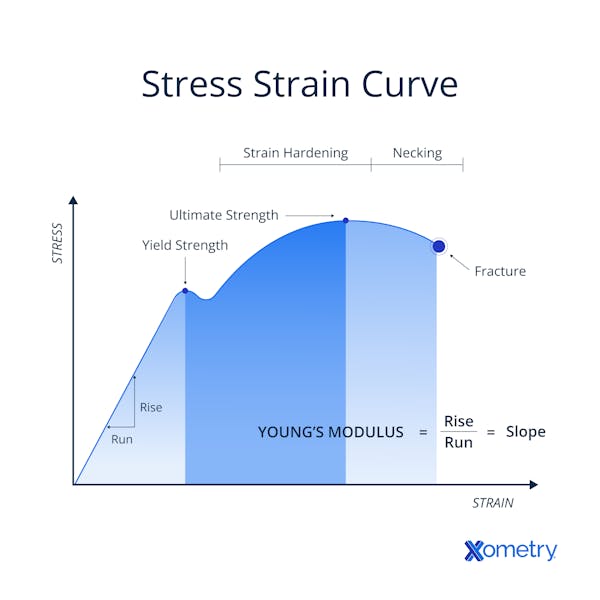
It is made up of a region where the material is elastic and returns to its original shape, a region where it is plastic and deforms permanently, and a region where it necks and experiences significant deformation and potential fracture. When designing and engineering materials for different applications, it is a crucial tool for engineers and materials scientists.
What Is Strain in Hooke's Law?
According to Hooke's law, strain is the degree of elastic material deformation that results from the application of a force. In more detail, strain is defined as the ratio of a material’s changed length to its initial length. A material may change in size or shape when subjected to a force, and the amount of strain it undergoes is determined by the strength of the applied force and the characteristics of the material. The modulus of elasticity, also known as Young’s modulus, is a material characteristic that describes how much a material will deform under a specific amount of stress. It describes the relationship between the amount of strain and the amount of stress applied. Mathematically, strain is represented as:
ε = ΔL / L₀
What Are the Benefits of Strain Analysis in Mechanics?
Among the advantages of strain analysis in mechanics are the following:
- Ability to predict material behavior under load (evaluation of material properties such as Young's modulus and Poisson's ratio)
- Design of safe and efficient structures
- Analysis of deformation and failure mechanisms
- Optimization of manufacturing processes for specific materials and applications
What Are the Limitations of Strain Analysis in Mechanics?
The following are some of the limitations of strain analysis in mechanics:
- External elements like vibration, electromagnetic interference, and other environmental elements can have an impact on strain measurements. This can make it challenging to measure strain accurately in some circumstances.
- Although strain is an important idea in mechanics, it only represents a small portion of the whole. Other elements, including stress, are crucial in describing how materials behave when they are under load.
- Strain analysis has limited applicability for nonlinear material behavior, especially when materials do not follow linear-elastic assumptions.
- Temperature is an additional factor that can (a) cause strain in materials, independent of externally applied forces; or (b) cause the relationship between stress and strain to change with temperature, and become more difficult to predict in some cases.
Is Tensile Stress the Same as Tensile Strain?
No, tensile stress and strain are not the same. Tensile stress is the amount of force per unit area applied in a direction normal to the cross-section of interest, while tensile strain is the material's elastic or plastic deformation response to the application of a tensile force. However, the two quantities, tensile stress and tensile strain, are related to each other by the elastic modulus of the material. Young’s Modulus, calculated as stress divided by strain in the elastic regime, characterizes a material’s stiffness.
Is Shear Stress the Same as Shear Strain?
No, shear strain and shear stress are not the same. Shear strain is the shape change caused by an applied shear force, whereas shear stress is the force per unit area applied parallel to a cross-sectional surface of interest.
Summary
This article presented strain, explained what it is, and discussed how to calculate it. To learn more about strain, contact a Xometry representative.
Xometry provides a wide range of manufacturing capabilities and other value-added services for all of your prototyping and production needs. Visit our website to learn more or to request a free, no-obligation quote.
Disclaimer
The content appearing on this webpage is for informational purposes only. Xometry makes no representation or warranty of any kind, be it expressed or implied, as to the accuracy, completeness, or validity of the information. Any performance parameters, geometric tolerances, specific design features, quality and types of materials, or processes should not be inferred to represent what will be delivered by third-party suppliers or manufacturers through Xometry’s network. Buyers seeking quotes for parts are responsible for defining the specific requirements for those parts. Please refer to our terms and conditions for more information.


